The Graph Realization problem:

Graph Realization is the problem of constructing a tree from a set of its edge-labeled paths. More formally, Given subsets P₁,..P_n of {0,..,m-1}, find a tree T=(V,E) with E={0,..,m-1} such that every P_i is a path in T, or determine that no such tree exists.

Graph Realization was first defined by Tutte [2]. Several polynomial algorithms for the problem were introduced in [1,3,4]. Graph Realization recently came back to awareness in computational molecular biology, in problems related to haplotype inference under the perfect phylogeny model [5].

About GREAL:

GREAL is an implementation of the algorithm for Graph Realization of Gavril and Tamari [1]. This algorithm runs in  O(nm²)time and  O(nm) space.

GREAL was written in C++. We supply here executables for Windows, Linux and SunOS. In addition to its standard interface, GREAL outputs the solution tree in a format that allows visualization using a graph drawing software [6].  See the Read Me file for details. 

GREAL was written by Tamar Barzuza, under the supervision by Dr. Itsik Pe’er, Prof. Jacques Beckmann (Weizmann Institute) and Prof. Ron Shamir (Tel Aviv University).

The GREAL software is freely available for academic use. Interested users (academic and commercial) should contact Ron Shamir (rshamir AT tau dot ac dot il)

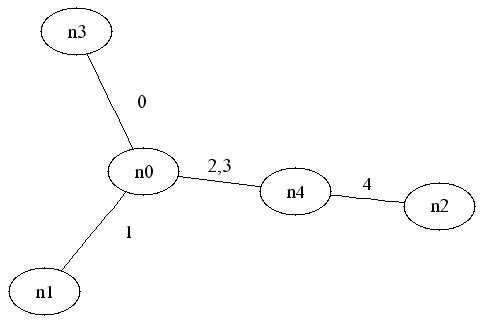
An example:

For the ground set {0,1,2,3,4}and the subests P₁={1,2,3,4},P₂={0,2,3} and P₃={0,1}, the graph realization is:

Notice that we merge a path of dependent edges into one edge, such as 2 and 3 in this example. Edges are dependent if they always appear together in P₁,..P_n.

Using the GREAL input and output formats (see  Read Me), the input  is the following hypergraph:

0	1	1	1	1
1	0	1	1	0
1	1	0	0	0

It indicates that E={0,..4} and that T must realize the paths {{1,2,3,4},{0,2,3},{0,1}}. This input is given in hypergraph.txt.

The output of GREAL is:

actual vertices:

0 = 0

1 = 1

2 = 2 3

3 = 4

realization:

-1 1 -1 0 2 1 -1 -1 -1 -1 -1 -1 -1 -1 3 0 -1 -1 -1 -1 2 -1 3 -1 -1

The realization matrix is the adjacency matrix of T. It indicates that V={0,..4} and that E is constructed form edges (0,1),(2,4),(0,3),(0,4) with initial labeling of 1,3,0,2 respectively.
The actual vertices list indicates that this labeling of E should be changed such that 0 remains 0, 1 remains 1, 2 is replaced by 2,3; and 3 is replaced by 4. The tree drawn above is a result of running neato on this output of GREAL.
 
For more details see the Read Me file. For a more complex example of a hypergraph see hypergraph.txt.

References: